flary's blog

机器学习-模型评估与选择（1）

发表于 | 分类于   |   字数统计: 4,697 字   |   阅读时长: 18 分钟

前沿

经小组协商，打算分工全方面、系统地学习机器学习的知识点。通过理论结合实践，从而达到对机器学习的本质有更加深入的了解，本篇博文参考《机器学习》西瓜书和李航老师的《统计学方法》，主要关于机器学习之模型评估与评估的一部分知识，后续更进补充。

统计学习三要素

统计学习(statistical learning) 是关于计算机基于数据构建概率统计模型并运用模型对数据进行预测与分析的一门学科，亦称为统计机器学习(statistical machine learning)。统计学习包括监督学习、非监督学习、半监督学习以及强化学习。统计学习方法都是由模型、策略、算法构成的，即统计学习的三要素，可以表示为：

方法 = 模型 + 策略 + 算法

  • 模型：指所要学习的条件概率分布或者决策函数，模型的假设空间包含所有可能的条件概率分布或决策函数。决策函数表示的模型为非概率模型，条件概率表示的模型为概率模型。
  • 策略：有了模型的假设空间，策略就是要考虑按照什么样的准则学习或者选择最优的模型。

损失函数(loss function)或者代价函数(cost function)度量模型预测的好坏，风险函数(risk function)或者期望损失(expected loss)度量平均意义下模型预测的好坏，学习的目标就是选择期望风险最小的模型。模型关于训练数据集的平均损失称为经验风险(empirical risk)或者经验损失(empirical loss)，当样本容量N趋于无穷时，经验风险趋近于期望风险，所以很自然的想法是用经验风险估计期望风险。但是往往现实当中样本数目有限，经验风险最小化(empirical risk minimization，ERM)学习的效果就未必很好，会产生“过拟合(over-fitting)“现象，由此引出结构风险最小化(structural risk minimization，SRM)的策略，结构风险最小化等价于正则化(regularization)，结构风险小需要经验风险与模型复杂度同时小，结构风险小的模型往往对训练数据以及未知的预测数据都有较好的预测。经验风险函数或者结构风险函数就是最优化的目标函数。

  • 算法：从假设空间中选择最优模型，最后需要考虑的是用什么样的计算方法求解最优模型，而算法就指的是学习模型的具体计算方法。

这时，统计学习的问题归结为最优化问题。如果最优化问题有显示的解析解，这个最优化问题就比较简单。但通常解析解不存在，这就需要用数值计算的方法求解。如何保证找到全局最优解，并使得求解过程非常高效，就成为一个重要问题。

模型评估与选择

经验误差与过拟合

统计学习的目的是使学到的模型不仅对已知数据而且对未知数据都能有很好的预测能力。不同的学习方法会给出不同的模型，当损失函数给定时，基于损失函数的模型的训练误差和模型的测试误差就自然成为学习方法的评估标准。模型在训练集上的误差称为训练误差或者经验误差，在新样本上的误差称为测试误差或者泛化误差。显然，我们希望得到泛化误差小的学习器。

我们事先不知道新样本是什么样，实际能做的就是努力使经验误差最小化，为了达到这个目的，应该从训练样本中尽可能学出适用于所有潜在样本的”普遍规律”。在很多情况下，我们确实可以学得一个在训练集上表现很好的学习器，精度甚至可以达到100%，遗憾的是，这样的学习器在大多数情况下都不好。

当模型把训练样本学得”太好”的时候，很可能已经把训练样本本身的一些特点当做了所有潜在样本都会具有的一般性质，这样就会导致泛化性能下降，这种现象成为过拟合。

过拟合：也可以理解为在学习时选择的模型包含的参数过多，以致于出现对已知的数据预测得很好，但对未知数据预测得很差的现象。

评估方法

通常，我们可以通过实验测试来对模型的泛化误差进行评估，进而做出选择。为此，需要一个”测试集”来测试模型对新样本的判别能力，然后以测试集上的测试误差作为泛化误差的近似。
通常我们假设测试样本也是从样本真实分布中独立同分布采样得到，但测试集应该尽可能与训练集互斥。一个只有m个样本的数据集D，既要训练，又要测试，那就要对D进行适当的划分处理，下面介绍几种方法：

留出法(hold-out)

直接将数据集D划分为两个互斥的集合，其中一个作为训练集S，另一个作为测试集T。在S上训练模型后，用T来评估测试误差，作为对泛化误差的估计。需要注意的三点：

  • 训练/测试集的划分要尽可能保持数据分布的一致性，例如在分类问题中至少要保持样本的类别比例相似（分层采样）。
  • 即使给出划分比例，划分的结果也有多种，一般要采用若干次随机划分、重复进行实验评估后取平均值。
  • 测试集小的话，评估结果的方差较大；训练集小的话，评估结果的偏差较大。所以通常将大约2/3~4/5的样本用于训练，剩余样本用于测试。

交叉验证法(cross validation)

将数据集D划分为k个大小相似的互斥子集，每个子集尽可能保持数据分布一致性（分层采样）。每次用k-1个子集的并集作为训练集，余下的那个子集作为测试集，从而可以用k组训练/测试集分别进行训练和测试，得到k个测试结果的均值，该过程称为k折交叉验证(k-fold cross validation)。k通常取值为10，即10折交叉验证。

  • 同样，为避免划分不同引入的差别，k折交叉验证通常也要随机使用不同的划分重复p次，最终的评估结果是p次k折交叉验证结果的均值。
  • 特例，留一法(leave one out，LOO)：测试集只包含一个样本，优点是偏差小，评估结果往往被认为比较准确，缺点是模型过多，计算开销太大。
1
2
3
4
5
6
7
8
9
10
11
12
13
# k折交叉验证
import numpy as np
from sklearn.model_selection import KFold
X = np.array([[0., 0.], [1., 1.], [-1., -1.], [2., 2.]])
y = np.array([0, 1, 0, 1])
X_train, X_test, y_train, y_test = X[train], X[test], y[train], y[test]
kf = KFold(n_splits=2)    # k = 2
for train, test in kf.split(X):
    print("%s %s" % (train, test))
    X_train, X_test, y_train, y_test = X[train], X[test], y[train], y[test]
>>> out:
[2 3] [0 1]
[0 1] [2 3]
1
2
3
4
5
6
7
8
9
10
11
# 留一法
from sklearn.model_selection import LeaveOneOut
X = [1, 2, 3, 4]
loo = LeaveOneOut()
for train, test in loo.split(X):
    print("%s %s" % (train, test))
>>> out:
[1 2 3] [0]
[0 2 3] [1]
[0 1 3] [2]
[0 1 2] [3]
1
2
3
4
5
6
7
8
9
10
11
#分层k折交叉验证
from sklearn.model_selection import StratifiedKFold
X = np.ones(10)
y = [0, 0, 0, 0, 1, 1, 1, 1, 1, 1]
skf = StratifiedKFold(n_splits=3)    # k = 3
for train, test in skf.split(X, y):
    print("%s %s" % (train, test))
>>> out:
[2 3 6 7 8 9] [0 1 4 5]
[0 1 3 4 5 8 9] [2 6 7]
[0 1 2 4 5 6 7] [3 8 9]

自助法(bootstrapping)

在留出法和交叉验证法中，都保留了一部分样本用于测试，这必然会引入因训练规模不同而导致的偏差，自助法可以避免这个问题。

自助法以自助采样为基础。给定包含m个样本的数据集D，每次从D中挑选一个样本，将其拷贝放入D’中，然后放回D，使得该样本下次还有被挑中的可能；重复该过程m次，我们就得到了m个样本的数据集D’。显然D中有一部分样本会在D’中多次出现，而另一部分样本不会出现。统计可知，初始数据集D中约有36.8%的样本未出现在D’中。D’当作训练集（m个样本），D/D’用作测试集。

  • 在数据集较小、难以有效划分训练/测试集时，自助法很有用。
  • 自助法可以通过多次采样产生多个不同的训练集，一般用于集成学习。
  • 自助法产生的数据集改变了初始数据集的分布，这会引入偏差，因此，数据量大时，一般使用留出法和交叉验证法。

调参与最终模型

大多数学习算法都有参数(parameter)需要设定，在模型评估与选择时候，除了要对算法进行选择，还要对算法参数进行设定，即为”调参(parameter tunning)”。

  • 学习算法的参数在实数范围内取值的，选参通常是对每个参数选定一个范围和变化步长，如在[0，0.2]区间内以0.05为步长，则候选参数为5个。
  • 在模型选择完成后，学习算法和参数就已经选定了，此时应该用全量数据集重新训练一遍模型，这才是最终的模型。
  • 通常把模型在实际应用中遇到的数据称为测试数据，而模型评估与选择中用于评估测试的数据集称为”验证集(validation set)”。即，测试集上的效果判别模型的泛化能力，训练数据划分为训练集和验证集，基于验证集上的效果来进行模型选择和调参。

性能评估

对模型的评估，不仅需要有效的估计方法，还需要有衡量模型泛化能力的指标，这就是性能度量(performance measure)。

回归预测常用的性能度量

  • 均方误差(mean squared error)

    1
    2
    3
    4
    5
    6
    from sklearn.metrics import mean_squared_error
    y_true = [3, -0.5, 2, 7]
    y_pred = [2.5, 0.0, 2, 8]
    mean_squared_error(y_true, y_pred)
    >>> out:
    0.375

  • 平均绝对误差(mean absolute error)

    1
    2
    3
    4
    5
    6
    from sklearn.metrics import mean_absolute_error
    y_true = [3, -0.5, 2, 7]
    y_pred = [2.5, 0.0, 2, 8]
    mean_absolute_error(y_true, y_pred)
    >>> out:
    0.5

  • 解释方差得分(explained variance score)

    其中，Var是方差，最好的得分是 1，值越低越差。

    1
    2
    3
    4
    5
    6
    from sklearn.metrics import explained_variance_score
    y_true = [3, -0.5, 2, 7]
    y_pred = [2.5, 0.0, 2, 8]
    explained_variance_score(y_true, y_pred)
    >>> out:
    0.95717344753747324

  • 可决系数(R2 score)

    其中，

    它提供了将来样本如何可能被模型预测的估量。最佳分数为1，可以为负数（因为模型可能会更糟）。

    1
    2
    3
    4
    5
    6
    from sklearn.metrics import r2_score
    y_true = [3, -0.5, 2, 7]
    y_pred = [2.5, 0.0, 2, 8]
    r2_score(y_true, y_pred)
    >>> out:
    0.94860813704496794

分类问题常用的性能度量

  • 错误率与精度
    错误率是分类错误的样本数占总数的比例，精度则是分类正确的样本占总数的比例，即为：

    其中，$1(x)$是0-1指示函数。

    1
    2
    3
    4
    5
    import numpy as np
    from sklearn.metrics import accuracy_score
    accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
    >>> out:
    0.5

  • 查准率、查全率
    对于二分类问题，可以将样例划分为真正例(true positive)、假正例(false positive)、真反例(true negative)、假反例(false negative)四种情形，令TP、FP、TN、FN分别为其对应的样本数，显然TP + FP + TN + FN = 样本总数。
    查准率P：在所有预测为正样本的样本(TP+FP)中预测正确(TP)的比例，
    查全率R：在所有正样本(TP+FN)中，预测正确(TP)的比例。

    通常，两者往往是一对矛盾的度量，查准率高时，查全率偏低；查全率高时，查准率偏低，只有在一些简单的任务中，两者才可能都高。

    1
    2
    3
    4
    5
    6
    7
    # 混淆矩阵
    from sklearn.metrics import confusion_matrix
    y_true = [0, 0, 0, 1, 1, 1, 1, 1]
    y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
    tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel()
    >>> out:
    (2, 1, 2, 3)

  • F1分数
    为了综合考虑查准率与查全率，于是有了F1度量：

    F1是基于查准率与查全率的调和平均，在一些应用中，对查准率和查全率的重视程度有所不同，因此，有F1加权的一般形式为：

    $\beta$度量了查全率对查准率的相对重要性，$\beta = 1$就是标准的F1；$\beta > 1$时查全率影响更大，反之，查准率影响更大。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    #分类指标报告
    from sklearn.metrics import classification_report
    y_true = [0, 1, 2, 2, 0]
    y_pred = [0, 0, 2, 1, 0]
    target_names = ['class 0', 'class 1', 'class 2']
    print(classification_report(y_true, y_pred, target_names=target_names))
    >>> out:
                 precision    recall  f1-score   support

        class 0       0.67      1.00      0.80         2
        class 1       0.00      0.00      0.00         1
        class 2       1.00      0.50      0.67         2

    avg / total       0.67      0.60      0.59         5

  • ROC与AUC
    ROC(receiver operating characteristic)曲线的提出是考虑模型在不同任务下的”期望泛化误差”的好坏。
    “真正率”(true positive rate, TPR)：正确分类的正样本占所有正样本的比例
    “假正率”(false positive rate, FPR)：误分类为正样本占所有负样本的比例。

    ROC曲线就是当将预测结果分割为正负样本的阈值变化时，以FPR作为x轴，以TPR作为y轴得到的曲线，ROC曲线下的面积即为AUC(area under ROC curve)，如下图基于有限预测样本的图：
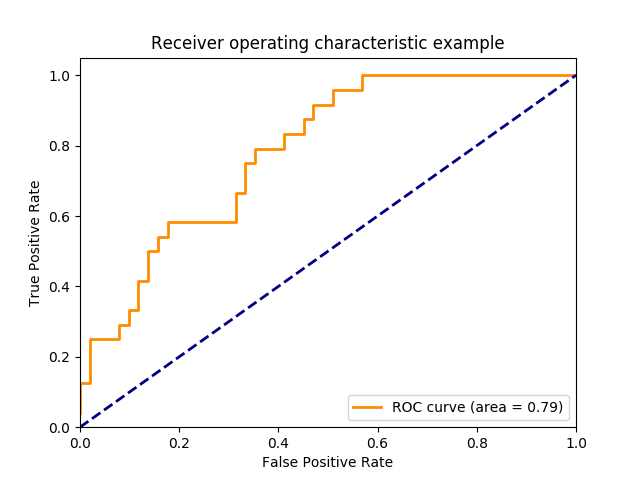
    Alt text

    ROC曲线中的四个点和一条线:
    (0,1)：即FPR=0，TPR=1，FN＝FP＝0，将所有的样本都正确分类；
    (1,0)：即FPR=1，TPR=0，最差分类器，避开了所有正确答案；
    (0,0)：即FPR=TPR=0，FP＝TP＝0，分类预测所有的样本都为负样本；
    (1,1)：即FPR=TPR=1，FN=TN＝0，分类预测所有的样本都为正样本。
    总之：ROC曲线越接近左上角，该分类器的性能越好。
    AUC的情况：
    AUC = 1：绝对完美分类器，理想状态下，100%完美识别正负类；
    0.5<AUC<1：优于随机猜测。这个分类器妥善设定阈值的话，可能有预测价值；
    AUC=0.5：跟随机猜测一样，模型没有预测价值；
    AUC<0.5：比随机猜测还差；只要反预测就优于随机猜测，不存在该状况。
    总之：AUC值越大的分类器，正确率越高。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# ROC
import numpy as np
from sklearn.metrics import roc_curve
y = np.array([1, 1, 2, 2])
scores = np.array([0.1, 0.4, 0.35, 0.8])
fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2)
>>> fpr
array([ 0. ,  0.5,  0.5,  1. ])
>>> tpr
array([ 0.5,  0.5,  1. ,  1. ])
>>> thresholds
array([ 0.8 ,  0.4 ,  0.35,  0.1 ])
# AUC
import numpy as np
from sklearn.metrics import roc_auc_score
y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
roc_auc_score(y_true, y_scores)
>>> out:
0.75

既然已经这么多评价标准，为什么还要使用ROC和AUC呢？因为ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反）

  • 对数损失
    对数损失(Log loss)亦被称为逻辑回归损失(Logistic regression loss)或交叉熵损失(Cross-entropy loss)。
    对于具有真实标签 $y \in {0,1}$ 的二分类和概率估计$p = \rm{Pr}(y = 1)$， 每个样本的log loss是给定的分类器的negative log-likelihood真正的标签:

  • 铰链损失
    铰链损失(hinge loss)函数使用hinge loss计算模型和数据之间的平均距离，这是一种只考虑预测误差单向指标，用于最大边界分类器，如支持向量机。
    铰链损失最开始出现在二分类问题中，假设正样本被标记为1，负样本被标记为-1，$y$是真实值，$w$是预测值，则铰链损失定义为：

    然后被扩展到多分类问题，假设$y_w$是对真实分类的预测值，$y_t$是对非真实分类预测中的最大值，则铰链损失定义为：

  • 海明距离
    海明距离(Hamming Distance)用于需要对样本多个标签进行分类的场景。对于给定的样本$i$，$L$是标签数量，则第$i$个样本的的海明距离为：

    其中$1(x)$是指示函数。当预测结果与实际情况完全相符时，距离为0；当预测结果与实际情况完全不符时，距离为1；当预测结果是实际情况的真子集或真超集时，距离介于0到1之间。
    我们可以通过对所有样本的预测情况求平均，得到算法在测试集上的总体表现情况，当标签数量$L$为1时，它等价于精度(Accuracy)，当标签数$L>1$时也有较好的区分度，不像准确率那么严格。

  • 杰卡德相似系数
    杰卡德相似系数(Jaccard similarity coefficients)也是用于需要对样本多个标签进行分类的场景。对于给定的样本$i$，$\hat{y}_i$是预测结果，${y}_i$是真实结果，$L$是标签数量，则第$i$个样本的杰卡德相似系数为：

    它与海明距离的不同之处在于分母。当预测结果与实际情况完全相符时，系数为1;当预测结果与实际情况完全不符时，系数为0;当预测结果是实际情况的真子集或真超集时，距离介于0到1之间。
    同样可以通过对所有样本的预测情况求平均得到算法在测试集上的总体表现情况，当标签数量$L$为1时，它等价于精度(Accuracy)。

后续检验方法，未待完续...

-------------本文结束感谢您的阅读-------------
友情提示: 转载请保留原文链接及作者。

感谢支持、勇于创作