改进神经网络的学习方法(1)

本资料摘自于《神经网络与深度学习》一文，总结了一下其中提到的改进学习的方法，方法仅仅覆盖了大量已经在神经网络中研究发展出的技术的一点点内容。掌握了这些关键技术不仅仅对这些技术本⾝的理解很有用，而且会深化对使用神经网络时会遇到哪些问题的理解。

交叉熵代价函数

众所周知，神经元是通过改变权重和偏置，并以⼀个代价函数的偏导数（$\partial C/\partial w$ 和 $\partial C/\partial b$）决定的速度学习。所以，我们在说“学习慢”时，实际上就是说这些偏导数很小。理解他们为何这么小就是我们面临的挑战。为了理解这些，让我们计算偏导数看看。二次代价函数如下：

$C(w,b) = \frac{1}{2n}\sum_{x}||y(x) - a||^2$

假设有个小例⼦，包含一个只有一个输入的神经元，让输入1转化为0。则对应的二次代价函数为：

$C = \frac{(y-a)^2}{2}$

其中a是神经元的输出，训练输入为$x = 1$，$y = 0$则是目标输出。显式地使用权重和偏置来表达这个，我们有$a = \sigma(z)$，其中$z = wx + b$。使用链式法则来求权重和偏置的偏导数就有：

$\frac{\partial C}{\partial w} = (a-y) \sigma \prime(z)x = a\sigma \prime(z)$ $\frac{\partial C}{\partial b} = (a-y) \sigma \prime(z) = a\sigma \prime(z)$

当神经网络的激活函数是sigmoid函数时，函数曲线在取值为1的附近变得相当平，所以$ \sigma \prime(z)$就很小了。因此上式的偏导数会非常小。这其实就是学习缓慢的原因所在。这种学习速度下降的原因实际上也是更加一般的神经网络学习缓慢的原因，并不仅仅是在这个特例中特有的。

那么我们如何解决这个问题呢？

假设，我们现在要训练一个包含若干输入变量的的神经元，目标输出y都是0或1。神经元的输出$a = \sigma(z)$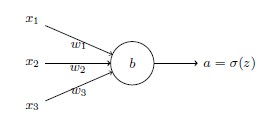

其中：

$z =\sum_{j}w_jx_j + b$

是输入的带权和，如下定义这个神经元的交叉熵代价函数：

$C = -\frac{1}{n}\sum_{x}[y \ln a + (1-y)\ln(1-a)]$

其中n是训练数据的总数，求和是在所有的训练输入x上进行的，y是对应的目标输出。

将交叉熵看做是代价函数有两点原因：

它是非负的，C > 0。
若对于所有的训练输入x，神经元实际的输出接近目标值，那么交叉熵将接近0。

但是交叉熵代价函数有一个比二次代价函数更好的特性就是它避免了学习速度下降的
问题。为了弄清楚这个情况，我们来算算交叉熵函数关于权重的偏导数，得到：

$\frac{\partial C}{\partial w_j} = \frac{1}{n} \sum_{x} \frac{\sigma \prime(z)x_j}{\sigma(z)(1-\sigma(z))} (\sigma(z) - y)$

根据$\sigma(z) = 1/(1+e^{-z})$的定义，可以得到$\sigma \prime(z) = \sigma(z)(1-\sigma(z))$。代入上式可得：

$\frac{\partial C}{\partial w_j} = \frac{1}{n} \sum_{x} x_j(\sigma(z) - y)$

这是一个优美的公式。它告诉我们权重学习的速度受到$\sigma(z) - y$影响，也就是输出中的误差的控制。更大的误差，更快的学习速度，这是我们直觉上期待的效果。特别地，这个代价函数避免了像在二次代价函数中求$\sigma \prime(z)$导致学习缓慢的问题。类似的方法，我们可以计算出关于偏置的偏导数：

$\frac{\partial C}{\partial b} = \frac{1}{n} \sum_{x} (\sigma(z) - y)$

那么我们应该在什么时候用交叉熵来替换⼆次代价函数？实际上，如果输出神经元是S型神经元(如sigmoid函数)时，交叉熵一般都是更好的选择。

注意：

对其他的问题（如回归问题）y 可以取0和1之间的中间值的。其实，交叉熵对所有训练输入在$\sigma(z) = y$时仍然是最小化的。此时交叉熵的表示是： $C = -\frac{1}{n}\sum_{x}[y \ln y + (1-y)\ln(1-y)]$ 其中$-[y \ln y + (1-y)\ln(1-y)]$有时候被称为二元熵。
交叉熵避免了学习缓慢的问题，不仅仅是在一个神经元上，且在多层多元网络上都起作。这个分析过程稍作变化对偏置也是一样的。
如果输出神经元是线性的，不再是S型函数作用的结果，那么二次代价函数不再会导致学习速度下降的问题。在此情形下，二次代价函数就是一种合适的选择。

使用交叉熵来对MNIST数字进行分类：

import mnist_loader
>>> training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
# 学习30次迭代期，小批量数据大小为10，学习速率 = 0.5
>>> net.SGD(training_data, 30, 10, 0.5, evaluation_data=test_data,monitor_evaluation_accuracy=True)
# 最高准确率：
# Epoch 26 training complete
# Accuracy on evaluation data: 9550 / 10000

softmax

softmax的想法其实就是为神经网络定义一种新式的输出层。开始时和S型层一样的，首先计算带权输入z，不过不会使用S型函数作用获得输出，而是用一个叫softmax的函数作用在z上获得输出，根据这个函数，第j个神经元的输出就是：

$a_j^L = \frac{e^{z_j^L}}{\sum_k e^{z_j^L}}$

其中，分母中的求和是在所有输出神经元上进行的，不难看出，输出激活值都是正数，而且激活值加起来正好为1。

因此，softmax层的输出可以被看做是一个概率分布。这样的效果很令人满意，在很多问题中，能够将输出激活值a理解为网络对于正确输出为的概率的估计是非常方便的。

softmax的一些性质：

具有单调性。
非局部性，任何特定的输出激活值依赖所有带权输入。

作为一种更加通用的视角，softmax + 对数似然代价函数的组合，更加适用于那些需要将输出激活值解释为概率的场景。

过拟合和规范化

过度拟合是神经网络的一个主要问题。这在现代网络中特别正常，因为网络权重和偏置数量巨大。为了高效地训练，我们需要一种检测过度拟合是不是发生的技术，这样我们不会过度训练，并且我们也想要找到一些技术来降低过度拟合的影响。看一个例子：

>>> import mnist_loader
>>> training_data, validation_data, test_data =  mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
# 学习400次迭代期，小批量数据大小为10，学习速率 = 0.5，只用1000幅图像
>>> net.SGD(training_data[:1000], 400, 10, 0.5, evaluation_data=test_data, monitor_evaluation_accuracy=True, monitor_training_cost=True)

我们可以画出当网络学习时代价变化的情况：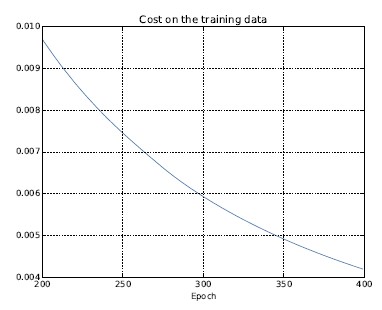

以及分类准确率在测试集上的表现：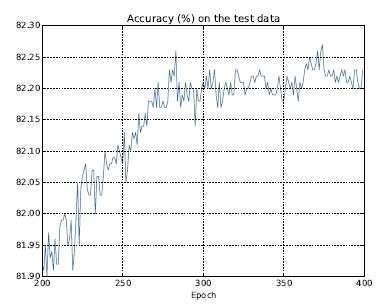

可以看出，网络在280迭代期后就过度拟合（overfitting）或者过度训练了。

检测过度拟合的明显方法是—— 跟踪测试数据集合上的准确率随训练变化情况。如果我们看到测试数据上的准确率不再提升，那么我们就停止训练。使用验证集检验模型是否过拟合是一般的做法。

L2规范化

一般来说，最好的降低过拟合的方式之一是增加训练样本量，有了足够的训练数据，就算是一个规模非常大的网络也不太容易过拟合，但不幸的是，训练数据其实是很难或者很昂贵的资源，所以这不是一种太切合实际的选择。

其实，还有其他的技术能够缓解过拟合，即使我们只有一个固定的网络和固定的训练集合，而这种技术就是规范化。最为常见的规范化手段被称为权重衰减或者L2规范化。L2 规范化的想法是增加⼀个额外的项到代价函数上，这个项叫做规范化项。下面是规范化的交叉熵代价函数：

$C = -\frac{1}{n}\sum_{x_j}[y_j \ln a_j^L + (1-y_j)\ln(1-a_j^L)]+\frac{\lambda}{2n}\sum_w w^2$

其中，第一项就是常规的交叉熵表达式，第二项加入的就是所有权重的平方的和，然后使用一个因子进行量化调整，其中 $\lambda> 0$ 可以称为规范化参数。（当然，对其他的代价函数也可以进⾏规范化）。都可以写成以下形式：

$C=C_0 + \frac{\lambda}{2n}\sum_w w^2$

现在，对于这样的规范化为何能够减轻过度拟合还不是很清楚，首先我们需要知道如何计算对网络中所有权重和偏置的偏导数：

$\frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} w$ $\frac{\partial C}{\partial b} = \frac{\partial C_0}{\partial b}$

权重的学习规则就变成：

$w = w - \eta \frac{\partial C_0}{\partial w} - \frac{\eta \lambda}{n} w = (1- \frac{\eta \lambda}{n}) w - \eta \frac{\partial C_0}{\partial w}$

这正和通常的梯度下降学习规则相同，除了通过一个因子$1- \frac{\eta \lambda}{n}$重新调整了权重w。这种调整有时被称为权重衰减，因为它使得权重变小了。通常小的权重在某种程度上，意味着更低的复杂性，也就对数据给出了一种更简单却更强大的解释，因此应该优先选择。

规范化交叉熵代价函数的例子：

>>> import mnist_loader
>>> training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
# 30 个隐藏神经元、小批量数据大小为10，学习速率为0.5，400个迭代期，规范化参数lmbda=0.1
>>> net.SGD(training_data[:1000], 400, 10, 0.5, evaluation_data=test_data, lmbda = 0.1, monitor_evaluation_cost=True, monitor_evaluation_accuracy=True, monitor_training_cost=True, monitor_training_accuracy=True)

训练集上的代价函数持续下降：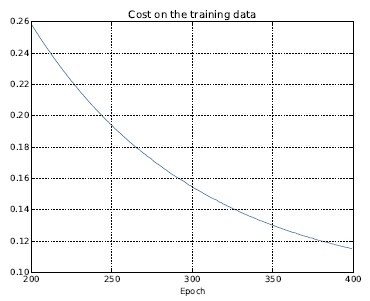

测试集上的准确率在整个400迭代期内持续增加：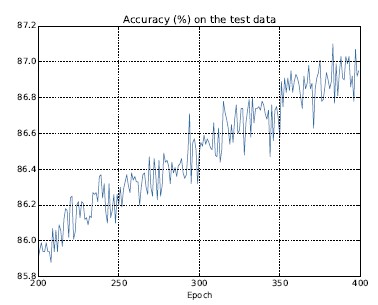

显然，规范化的使.能够解决过度拟合的问题。而且，准确率相当高了，相较于之前的82.27%，最高处达到了87.1%。

规范化的的其他技术

除了L2 外还有很多规范化技术。实际上，正是由于数量众多，也不会将所有的都列举出来。在本节，简要地给出三种减轻过度拟合的其他的方法：L1 规范化、弃权和人为增加训练样本。

L1 规范化：这个方法是在未规范化的代价函数上加上一个权重绝对值的和：

$C = C_0 + \frac{\lambda}{n} \sum_w |w|$

对应*L1 规范化代价函数的偏导数有：

$\frac{\partial C}{\partial w} = \frac{\partial C_0}{\partial w} + \frac{\lambda}{n} sgn(w)$

其中sgn(w) 就是w 的正负号，即w是正数时为+1，w为负数时为-1。使用这个表达式，我们可以轻易地对反向传播进行修改，从而使用基于L1规范化的随机梯度下降进行学习。对L1规范化的网络进行更新的规则就是：

$w = w - \eta \frac{\partial C_0}{\partial w} - \frac{\eta \lambda}{n} sgn(w)$

L1和L2两种情形下，规范化的效果就是缩小权重。这符合我们的直觉，两种规范化都惩罚大的权重。但权重缩小的方式不同。在L1规范化中，权重通过一个常量向0进行缩小。在L2规范化中，权重通过一个和w成比例的量进行缩小的。

所以，当一个特定的权重绝对值|w|很大时，L1规范化的权重缩小得远比L2规范化要小得多。相反，当一个特定的权重绝对值|w|很小时，L1规范化的权重缩小得要比L2规范化大得多。最终的结果就是，L1规范化倾向于聚集网络的权重在相对少量的高重要度连接上，而其他权重就会被驱使向0接近。

注意：我在上面的讨论中其实忽略了一个问题—— 在w = 0 的时候，w偏导数未定义义。原因在于函数|w|在w = 0 时有个“直角”，事实上，导数是不存的。不过没关系，我们要做的就是应用通常的（无规范化的）随机梯度下降的规则在w = 0处，更确切地说，我们约定sgn(0) = 0。

弃权：弃权（Dropout）是一种相当激进的技术。和L1、L2规范化不同，弃权技术并不依赖对代价函数的修改。而是，在弃权中，我们改变了网络本身，先描述一下弃权基本的工作机制。我们尝试训练一个网络：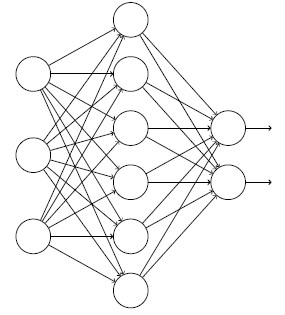

假设我们有一个训练数据x和对应的目标输出y。通常我们会通过在网络中前向传播x，然后进行反向传播来确定对梯度的贡献。使用弃权技术，这个过程就改了。我们会从随机（临时）地删除网络中的一半的隐藏神经元开始，同时让输入层和输出层的神经元保持不变。在此之后，我们会得到最终如下线条所示的网络。注意那些被弃权的神经元，即那些临时被删除的神经元，用虚圈表示在图中：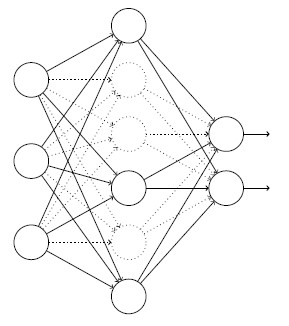

我们前向传播输入x，通过修改后的网络，然后反向传播结果，在一个小批量数据样本上进行这些步骤后，对有关的权重和偏置进行更新，重置弃权的神经元，然后重复上述过程，最终网络会学到一个权重和偏置的集合。当然，这些权重和偏置也是在一半的隐藏神经元被弃权的情形下学到的。当实际运行整个网络时，是指两倍的隐藏神经元将会被激活。为了补偿这个，我们将从隐藏神经元出去的权重减半。

为什么弃权的方法能够进行规范化呢？启发式地看，当我们弃权掉不同的神经元集合时，有点像我们在训练不同的神经网络。所以，弃权过程就如同大量不同网络的效果的平均那样。不同的网络会以不同的方式过度拟合了，所以，弃权过的网络的效果会减轻过度拟合。弃权技术在训练大规模深度网络时尤其有效，这样的网络中过度拟合问题经常特别突出。

人为扩展训练数据：获取更多的训练样本其实是很好的想法。不幸的是，这个方法代价很.，在实践中常常是很难达到的。不过，还有一种方法能够获得类似的效果，那就是人为扩展训练数据，比如，旋转、转换、扭曲图像，对于语音识别，可以通过增加背景噪声来扩展数据等。

一般而言，准确率会随着更多的数据而不断增加。当然，在训练的后期，我们会发现学习已经接近饱和状态。

权重初始化

创建了神经网络后，我们需要进行权重和偏置的初始化。一种方式就是根据独立高斯随机变量来选择权重和偏置，其被归一化为均值为0，标准差1。这个方法还不错，但是非常特别，所以值得去重新探讨它，看看是否能寻找一些更好的方式来设置初始的权重和偏置，这也许能帮助我们的网络学习得更快。结果表明，我们可以使用比归一化的高斯分布做得更好的方法。

假设我们使用一个有大量输入神经元的网络，比如说1000个，并且训练输入x，其中一半的输入神经元值为1，另一半为0，已经使用了归一化的高斯分布初始化了连接隐藏层的权重，考虑隐藏神经元输入的带权和：

$z = \sum_j w_jx_j + b$

其中500个项消去了，因为对应的输入为0。所以z是遍历总共501个归一化的高斯随机变量的和，包含500个权重项和额外的1个偏置项。因此z本身是一个均值为0，标准差为$\sqrt {501}$ 的高斯分布。即，z是一个非常宽的高斯分布，分布图形完全不是很尖的形状，|z|会变得很大，这样隐藏神经元的输出$\sigma(z)$ 就会接近1或者0，也就表示我们的隐藏神经元会饱和。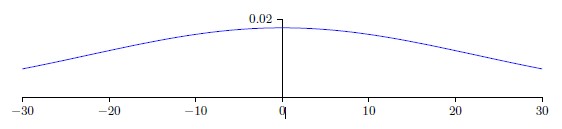

所以当出现这样的情况时，在权重中进行微小的调整仅仅会给隐藏神经元的激活值带来极其微弱的改变。而这种微弱的改变也会影响网络中剩下的神经元，然后会带来相应的代价函数的改变。结果就是，这些权重在我们进行梯度下降算法时会学习得非常缓慢。

解决方法：假设我们有一个n个输入权重的神经元，使用均值0，标准差$1/\sqrt n$的高斯分布初始化这些权重，也就是说会向下挤压图形，让神经元更不可能饱和，继续使用均值0标准差1的高斯分布对偏置进行初始化。

继续使用500个值为0的输入和500 个值为1的输入，很容易证明此时隐藏神经元输入的带权和z服从均值0，标准差为$\sqrt {3/2}$ 的高斯分布，这要比以前有更尖锐的峰值。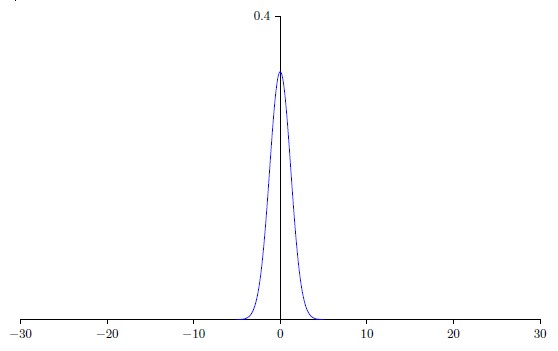

这样的一个神经元更不可能饱和，因此也不太可能遇到学习速度下降的问题。

MNIST 数字分类任务，使用30个隐藏神经元，小批量数据的大小为10，规范化参数5.0，然后是交叉熵代价函数，分别使用新旧权重初始化方法训练：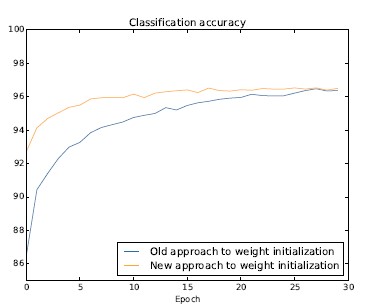

同样的情况使用100个隐藏神经元，得到：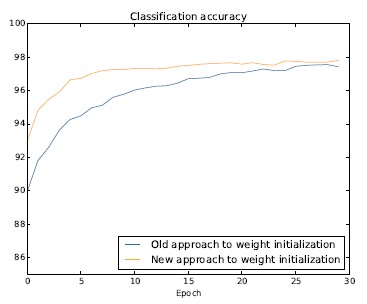

权重初始化不仅仅能够带来训练速度的加快，有时候在最终性能上也有所提升。

如何选择神经网络的超参数

直到现在，我们还没有解释对诸如学习速率 $\eta$，规范化参数 $\lambda$ 等等超参数选择的方法。

宽泛策略：在使用神经网络来解决新的问题时，一个挑战就是获得任何一种非寻常的学习，也就是说，达到比随机的情况更好的结果。这个实际上会很困难，尤其是遇到一种新类型的问题时。现在我们看看一些具体的设置超参数的推荐。

学习速率：假设我们运行了三个不同学习速率（0.025、0.25、2.5）的MNIST 网络，其他参数一致。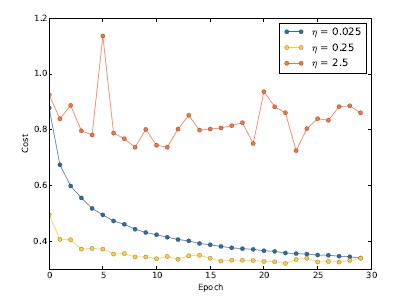

我们可以如下设置学习速率。首先，找到学习速率阈值的估计，它使得在训练数据上的代价立即开始下降而非震荡或者增加，这个估计并不需要太过精确，可以估计这个值的量级，比如说从等于0.01开始。

如果代价在训练前面若干回合开始下降，就可以逐步增大学习速率，比如0.1、1.0，直到若干回合代价开始震荡或者增加。相反，如果代价在学习速率等于0.01时就开始震荡或增加，那就减小它，比如0.001、0.0001，直到代价开始下降。

显然，学习速率实际值不应该比阈值大。实际上，更应该使用稍微小点的值，例如，阈值的一半这样的选择。

为何对学习速率要用训练代价来选择呢，而其他超参数用验证集？
原因就是其他的超参数倾向于提升最终的测试集上的分类准确率，所以将他们通过验证准确率来选择更合理一些。然而，学习速率仅仅是偶然地影响最终的分类准确率的，学习速率主要的目的是控制梯度下降的步长，监控训练代价是最好的检测步长过大的方法。

使用提前停止来确定训练的迭代期数量：提前停止表示在每个回合的最后，都要计算验证集上的准确率，当准确率不再上升，就终止它。