信贷评分卡模型

简介

评分卡是综合个人客户的多个维度信息（如基本情况、偿债能力、信用状况等，重点关注借贷意愿、偿债能力、还款意愿），基于这些信息综合运用数学分析模型，给个人综合评分，判断违约的可能性的工具。
信用评分卡模型在国外是一种成熟的预测方法，尤其在信用风险评估以及金融风险控制领域更是得到了比较广泛的使用，其原理是将模型变量WOE编码方式离散化之后运用logistic回归模型进行的一种二分类变量的广义线性模型。（就分析方法发而言，现在分类算法有很多种，决策树，逻辑回归，支持向量机，神经网络等等，都可以实现这个目的）。

评分卡是什么样子的？

芝麻信用的评分：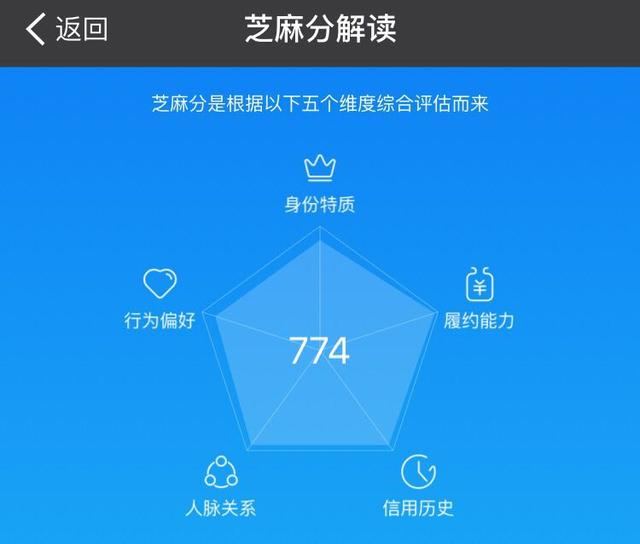

一个典型的贷前审批评分卡：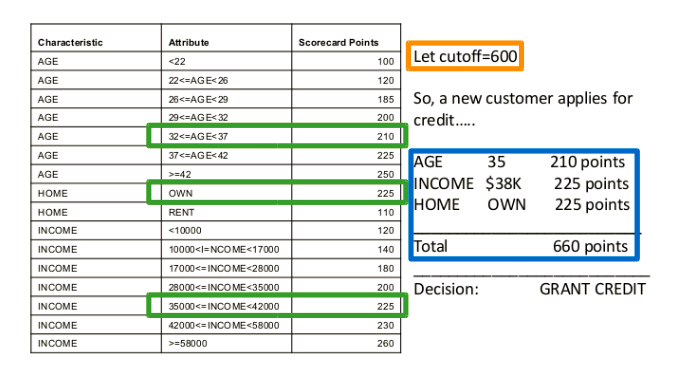

那么，问题来了：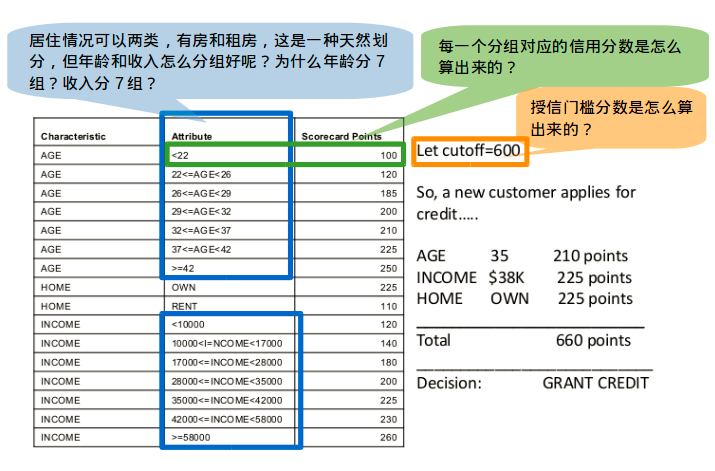

所以，评分卡设计围绕三个问题开展：

如何对年龄、收入这样的连续变量进行分组？
有了分组的结果后，每个分组应该给多少信用分？
如何定义一个合适的授信门槛分数？

基于Logistic回归的标准评分卡

由逻辑回归的基本原理，我们将客户违约的概率表示为p，则正常的概率为1-p。因此，可以得到违约和不违约的概率为：

$Odds = \frac{p}{1-p}$

其中，

$p(y=1\mid x) = \frac{1}{1+ \rm e^{-g(x)}}$ $p(y=0\mid x) = 1- p(y=1\mid x) = \frac{1}{1+ \rm e^{g(x)}}$

客户的违约概率也可以表示为：

$p = \frac{Odds}{1+Odds}$

评分卡设定的分值刻度可以通过将分值表示为比率对数的线性表达式来定义，即可表示为下式：

$Score = A-B*\log(Odds)$ $\log(Odds) = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \cdots + \beta_{n}x_{n}$

常数A、B的值可以通过将两个已知或假设的分值带入计算得到。通常情况下，需要设定两个假设：
（1）给某个特定的比率设定特定的预期分值；
（2）确定比率翻番的分数（PDO）

$P = A-B*\log(x)$ $P - PDO = A-B*\log(2*x)$

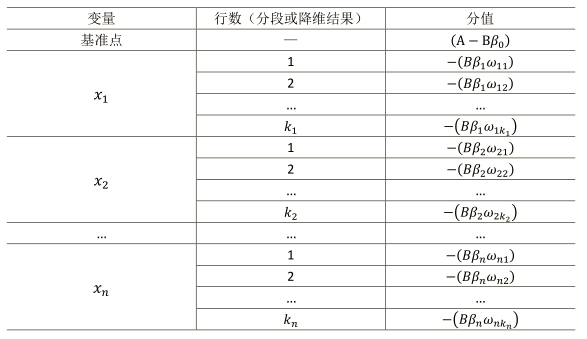
评分卡刻度参数A和B确定以后，就可以计算比率和违约概率，以及对应的分值了。通常将常数A称为补偿，常数B称为刻度。评分卡的分值可表达为：

$Score = A - B( \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \cdots + \beta_{n}x_{n})$

所有变量都用WOE进行转换，可得到：

$Score = (A - B\beta_{0})-(B\beta_{1}w_{11})\delta_{11}-(B\beta_{1}w_{12})\delta_{12}- \cdots \\ -(B\beta_{x}w_{x1})\delta_{x1} - (B\beta_{x}w_{x2})\delta_{x2} - \cdots$

式中wij为第i个变量第j个值的WOE，为已知变量；betai为逻辑回归方程中的系数，为已知变量；deltaij为二元变量，表示变量i是否取第j个值。此式即为最终评分卡公式。如果变量取不同行并计算其WOE值，式中表示的标准评分卡格式，如下表所示：

WOE 和 IV 详解

WOE

WOE（Weight of Evidence），即证据权重。WOE是对原始自变量的一种编码形式。要对一个变量进行WOE编码，需要首先把这个变量进行分组处理（也叫离散化、分箱等等）。

$WOE_{i} = \ln(\frac{py_{i}}{pn_{i}}) = \ln(\frac{\#y_{i}/\#y_{T}}{\#n_{i}/\#n_{T}})$

其中，pyi是这个组中响应客户（风险模型中，对应的是违约客户，总之，指的是模型中预测变量取值为“是”或者说1的个体）占所有样本中所有响应客户的比例，pni是这个组中未响应客户占样本中所有未响应客户的比例，#yi是这个组中响应客户的数量，#ni是这个组中未响应客户的数量，#yT是样本中所有响应客户的数量，#nT是样本中所有未响应客户的数量。

从公式中可知，WOE表示的实际上是“当前分组中响应客户占所有响应客户的比例”和“当前分组中没有响应的客户占所有没有响应的客户的比例”的差异。对这个公式做一个简单变换，可以得到：

$WOE_{i} = \ln(\frac{py_{i}}{pn_{i}}) = \ln(\frac{\#y_{i}/\#y_{T}}{\#n_{i}/\#n_{T}}) \\ = \ln(\frac{\#y_{i}/\#n_{i}}{\#y_{T}/\#n_{T}})$

变换以后我们可以看出，WOE也可以表示的是当前这个组中响应的客户和未响应客户的比值，和所有样本中这个比值的差异。这个差异是用这两个比值的比值，再取对数来表示的。WOE越大，差异越大，这个分组里的样本响应的可能性就越大，WOE越小，差异越小，这个分组里的样本响应的可能性就越小。
我们可以看一下WOE的基本特点：

当前分组中，响应的比例越大，WOE值越大；
当前分组WOE的正负，由当前分组响应和未响应的比例，与样本整体响应和未响应的比例的大小关系决定，当前分组的比例小于样本整体比例时，WOE为负，当前分组的比例大于整体比例时，WOE为正，当前分组的比例和整体比例相等时，WOE为0。
WOE的取值范围是全体实数。

WOE 和 OR的关系

OR，即Odds Ratio，是两组Odds的比值，比如age1和age2的Odds Ratio为：

$OR_{age2/age1} = \frac{Odds_{age2}}{Odds_{age1}} = \frac{p(y=1\mid Age = age2) / p(y=0\mid Age = age2)}{p(y=1\mid Age = age1) / p(y=0\mid Age = age1)}$

OR和Odds在logistic回归中非常值得重视，因为他们和参数的interpretation有关系，并且，当xi增加一个单位时，Odds将发生相应倍数增长：

$OR_{x_{i}+1/x_{i}} = \frac{Odds_{2}}{Odds_{1}} = \frac{p_{2} / 1-p_{2}}{p_{1} / 1-p_{1}}=\frac{\rm e^{\sum_{j \ne i}\beta_{j}x_{j} + \beta_{i}(x_{i}+1)}}{\rm e^{\sum_{j \ne i}\beta_{j}x_{j} + \beta_{i}x_{i}}}=\rm e^{\beta_{i}}$

通过条件概率公式转化可知：

$\ln\frac{p(y=1\mid age_{i})}{p(y=0\mid age_{i})} = \ln\frac{p(y=1)}{p(y=0)} + \ln\frac{p(age_{i}\mid y=1)}{p(age_{i}\mid y=0)}$

即：

$\ln(Odds_{age_{i}}) = 常数 + WOE_{age_{i}}$

因此，我们可以得到OR和WOE的关系为：

$\ln(OR_{age2/age1}) = WOE_{age2}- WOE_{age1}$

结论就是：如果使用了WOE编码，当我们对单变量进行回归（Y~Xi）时，可以不做dummy encoding，此时变量的系数恒为1。WOE编码起到了把回归系数“正则化”的作用。
下面用实例证明OR与WOE的关系。
WOE:

import pandas as pd
import numpy as np
df = pd.DataFrame({'X1':np.random.randint(3,size=1000),'y':np.random.randint(2,size=1000)})
table = pd.crosstab(df['y'],df['X1'])
woe_table = table.div(table.sum(axis=1),axis=0)
woe = (woe_table.iloc[1,:] / woe_table.iloc[0,:]).apply(lambda x:np.log(x))
print(woe[1]-woe[0])
print(woe[2]-woe[1])

OR:

OR_0_1 = np.log(1.0*table.iloc[0,0] * table.iloc[1,1] / table.iloc[0,1] / table.iloc[1,0])
OR_1_2 = np.log(1.0*table.iloc[0,1] * table.iloc[1,2] / table.iloc[0,2] / table.iloc[1,1])
print(OR_0_1)
print(OR_1_2)

IV的计算

IV（Information Value），中文意思是信息价值，或者信息量。
我们在用逻辑回归、决策树等模型方法构建分类模型时，经常需要对自变量进行筛选。那么我们怎么去挑选入模变量呢？需要考虑的因素很多，比如：变量的预测能力，变量之间的相关性，变量的简单性（容易生成和使用），变量的强壮性（不容易被绕过），变量在业务上的可解释性（被挑战时可以解释的通）等等。但是，其中最主要和最直接的衡量标准是变量的预测能力。我们需要一些具体的量化指标来衡量每自变量的预测能力，并根据这些量化指标的大小，来确定哪些变量进入模型。IV就是这样一种指标，它可以用来衡量自变量的预测能力。类似的指标还有信息增益、基尼系数等等。
基于上面的WOE，对于分组i，也会有一个对应的IV值，计算公式如下：

$IV_{i} = (py_{i}-pn_{i}) * WOE_{i} = (\#y_{i}/\#y_{T} - \#n_{i}/\#n_{T})\ln(\frac{\#y_{i}/\#y_{T}}{\#n_{i}/\#n_{T}})$

有了一个变量各分组的IV值，我们就可以计算整个变量的IV值，方法很简单，就是把各分组的IV相加：

$IV = \sum_{i}^{n} IV_{i}$

我们可以看出IV的以下特点：

对于变量的一个分组，这个分组的响应和未响应的比例与样本整体响应和未响应的比例相差越大，IV值越大，否则，IV值越小；
极端情况下，当前分组的响应和未响应的比例和样本整体的响应和未响应的比例相等时，IV值为0；
IV值的取值范围是$[0,+\infty)$，且，当当前分组中只包含响应客户或者未响应客户时，IV = $+\infty$。

实际应用中，通过IV值评判特征预测能力的标准如下：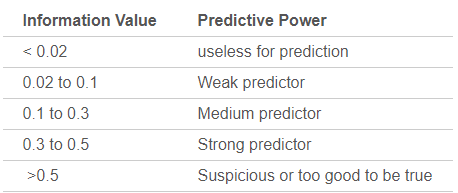

IV的极端情况以及处理方式

IV依赖WOE，并且IV是一个很好的衡量自变量对目标变量影响程度的指标。但是，使用过程中应该注意一个问题：变量的任何分组中，不应该出现响应数=0或非响应数=0的情况。
原因很简单，当变量一个分组中，响应数 = 0时：

$WOE_{i} = \ln(\frac{0/\#y_{T}}{\#n_{i}/\#n_{T}}) = -\infty$

而此时，$IV_{i}$为$+\infty$,
而当变量一个分组中，没有响应的数量 = 0时：

$WOE_{i} = \ln(\frac{\#y_{i}/\#y_{T}}{0/\#n_{T}}) = +\infty$

此时的$IV_{i}$也为$+\infty$，无论IV等于负无穷还是正无穷，都是没有意义的。
由上述问题我们可以看到，使用IV其实有一个缺点，就是不能自动处理变量的分组中出现响应比例为0或100%的情况。那么，遇到响应比例为0或者100%的情况，我们应该怎么做呢？建议如下：
（1）如果可能，直接把这个分组做成一个规则，作为模型的前置条件或补充条件。
（2）重新对变量进行离散化或分组，使每个分组的响应比例都不为0且不为100%，尤其是当一个分组个体数很小时（比如小于100个），强烈建议这样做，因为本身把一个分组个体数弄得很小就不是太合理。
（3）如果上面两种方法都无法使用，建议人工把该分组的响应数和非响应的数量进行一定的调整。如果响应数原本为0，可以人工调整响应数为1，如果非响应数原本为0，可以人工调整非响应数为1。

WOE和IV的意义何在？

变量替换为WOE值意义

对自变量进行分档，每档一个值来代表这段的自变量输入，通过转换后实现了稳定性要求；
克服不同变量间刻度不统一的问题，克服回归中缺失值的填充问题，很多极值变量通过WOE可以变为非异常值；
WOE能反映自变量的贡献情况，结合模型拟合出的系数和自变量内部WOE值的波动情况，构造出各个自变量的贡献率及相对重要性。一般地，系数越大，WOE的方差越大，则自变量的贡献率越大（类似于某种方差贡献率）。
WOE与违约概率具有某种线性关系，提升模型的预测效果，提高模型的可理解性
IV意义
衡量自变量的预测能力，从而进行特征选择。

讨论

评分卡是舶来品，对信用基础数据有一定要求，信用评分的建模过程更多地是分析的过程（而不是模型拟合的过程），也正因此，对模型参数的估计等等内容似乎并不做太多的学习，而把主要的精力集中于研究各个自变量与目标变量的关系，在此基础上对自变量做筛选和编码，最终再次评估模型的预测效果，并且对模型的各个自变量的效用作出相应的评价。
WOE 和 IV应用有局限性，这两个值的资料都是信用评分模型，机器学习的相关资料中很少关于这两个值的应用。
虽然网上到处都是神经网络、xgboost的文章，但当下的建模过程中（至少在金融风控领域）并没有完全摆脱logistic模型，原因大致有以下几点：
（1） logistic模型客群变化的敏感度不如其他高复杂度模型，因此稳健更好，鲁棒性更强。
（2）模型直观。系数含义好阐述、易理解。对金融领域高管以及银行出身的建模专家，变量系数可以跟他们的业内知识做交叉验证，更容易让人信服。
（3）也是基于2的模型直观性，当模型效果衰减的时候，logistic模型能更好的诊断病因。

参考资料：
https://www.jianshu.com/p/9eea3e8828b3
https://blog.csdn.net/kevin7658/article/details/50780391

简介