flary's blog

深度学习基础 - 从人工神经网络开始

发表于 | 分类于   |   字数统计: 3,952 字   |   阅读时长: 14 分钟

前言

深度学习（Deep Learning）目前是人工智能领域的大杀器，然而对于大多数研究者来说，对于深度神经网络的理解并不是很透彻，往往视其为黑盒子般的存在，包括本人，也只是知其然却不知其所以然。于是乎，从细节出发，本人决定好好探索深度学习中的奥妙。本文摘自analyticsvidhya上的一篇好文，该文对于从神经网络到深度学习的关键点有很细致、到位的理解。

介绍

深度学习（DL）和神经网络（NN）正推动着当今世纪的一些最具独创性的发明。它们难以置信的从数据和环境中学习的能力，使之成为科学家的首选。深度学习和神经网络是自动驾驶汽车，图像识别软件，推荐系统等产品的核心。显然，作为一种强大的算法，它对各种数据类型也具有高度的自适应性。
Alt text

目录

什么是神经网络？ 
单神经元如何工作？ 
为什么多层网络有用？
神经网络的一般结构
反向传播（非常重要）

什么是神经网络？

神经网络（NN）也被称为人工神经网络，是以人类神经系统运转的人工表示而命名的。首先我们来了解下神经系统是如何工作的，神经系统由数以百万计的神经细胞或神经元组成，神经元具有以下结构：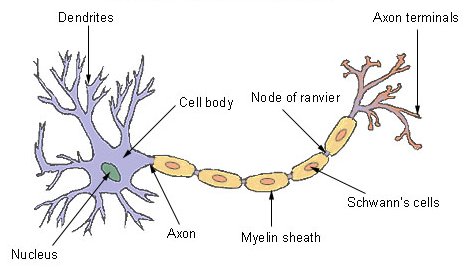
Alt text

它的主要组件包括：

  • 树突 - 它以电脉冲的形式从其他神经元获取输入。
  • 细胞体 - 它从这些输入生成推论并决定采取什么行动 。
  • 轴突终端 - 它以电脉冲的形式进行传输。

简而言之，每个神经元都通过树突从许多其他神经元接受输入。然后，对输入执行所需的处理，并通过轴突将另一个电脉冲发送到终端节点，从那里又传送给许多其他神经元。

ANN的工作方式非常相似。神经网络的一般结构如下所示：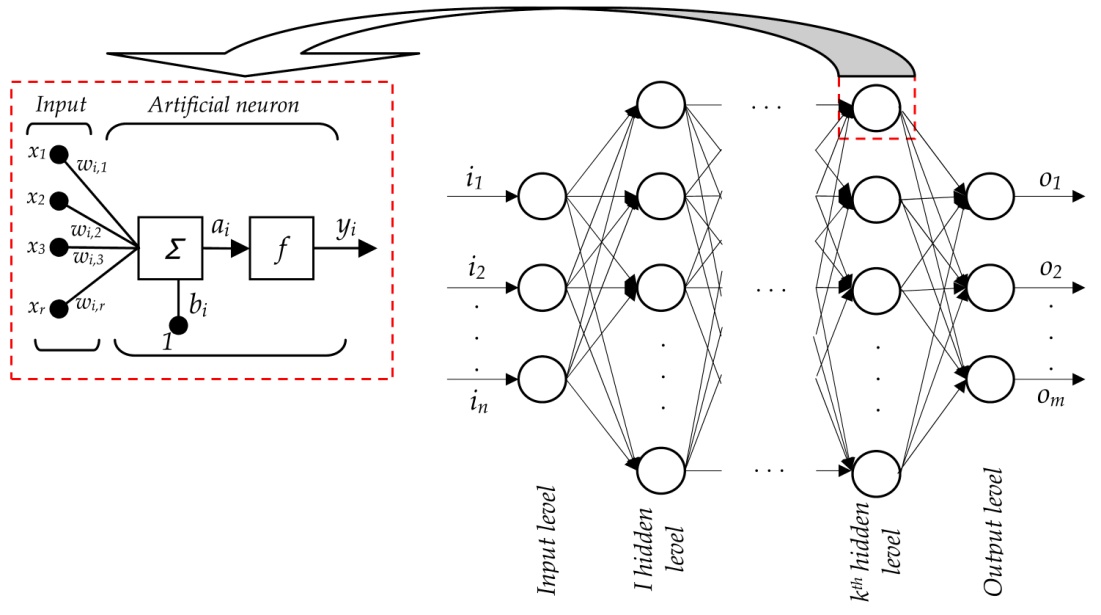
Alt text

上图红色框中单独描绘了单一神经元的典型神经网络结构。让我们来理解这一点，每个神经元的输入都是树突，就像在人类的神经系统中一样，一个神经元（虽然是人为的）集结所有的输入并对它们进行操作处理。然后，将输出传送给它所连接的其他神经元（即下一层）。神经网络层次分为3种类型：

  • 输入层：通过将观察样本传入到神经元。
  • 隐藏层：这是输入层和输出层之间的中间层，帮助神经网络学习数据中涉及的复杂关系。
  • 输出层：最后的输出是从前两层提取的。例如：对于一个5个类的分类问题，输出将会有5个神经元。

我们先通过例子来看看每个神经元的功能。

单神经元如何工作？

在本小节，透过简单的例子来了解单个神经元的工作机制，从而直观地理解神经元是如何通过使用输入来计算输出。单个神经元的神经网络结构如下：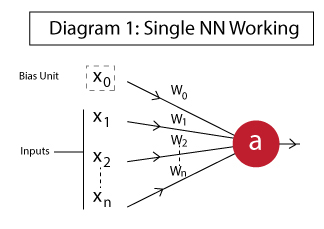
Alt text
与人类神经系统的神经元不同的是：

  • x1,x2,…,xN：神经元的输入。这些可以是来自输入层的实际观察值或来自某个隐藏层的中间值。
  • x0：偏置单元。它是一个组成激活函数变量的常量值。
  • a：神经元的输出，它按照以下公式计算得到：

这里，f 被称之为激活函数，它使得神经网络结构非常灵活，并且能够探索到数据中复杂的非线性关系。它可以是高斯函数，逻辑函数，双曲函数或甚至是简单的线性函数。

接下来，我们来实现神经网络中的3个基本函数：OR, AND, NOT，这有助于了解它们的内在本质。假设有一个分类问题，可以预测不同输入组合的输出（0或1），我们将使用以下激活函数对线性分类器进行建模：

实例：AND函数

AND函数可以这样实现：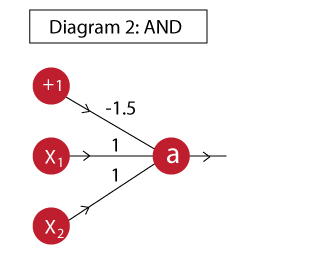
Alt text

该神经元的输出是：

它对应的真值表是：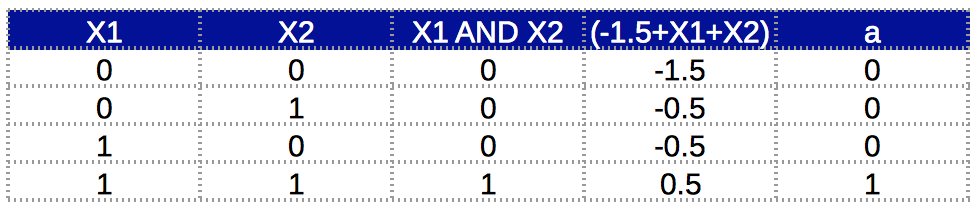
Alt text

我们可以看到，AND函数被成功实现了。列’a’和列’X1 AND X2’是一致的。我们注意到此时偏置项权重等于-1.5，但是它不是一个定值，直觉上，我们可以把它赋值为只有当$x_1$和$x_2$都是正数的情况下，并且满足总和为正数情况下的任何值。因此，当它取值（-1，-2）之间时满足要求。

实例：OR函数

OR函数可以这样实现：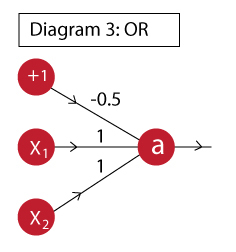
Alt text

该神经元对应的输出是：

它对应的真值表为：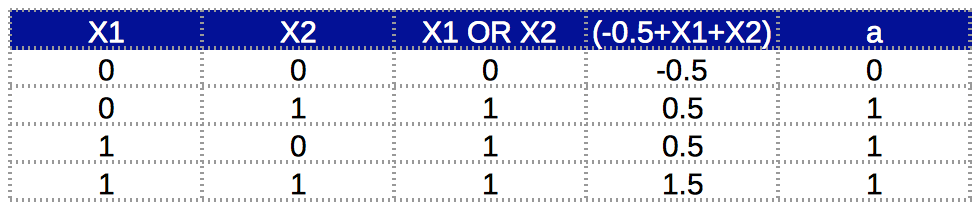
Alt text

列’a’和列’X1 OR X2’是一致的。我们可以看到，通过改变偏置项的权重，就可以实现OR函数了。这个上面的实例很相似，同样，可以直觉地认为偏置项权重取值为当$x_1$或$x_2$至少有一个正值，并满足总和为正数情况下的任何值。

实例：NOT函数

同上例一样，NOT函数可以如下被实现：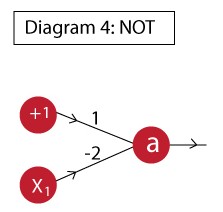
Alt text

该神经元对应的输出是：

它对应的真值表为：
Alt text

同样，输出符合NOT函数的表达式，相信通过这些例子，大概可以直观地了解神经网络中的神经元是如何工作的，上面的几个例子都是用了一个简单的激活函数。

注意：上面所用的简单激活函数往往会被替之为逻辑函数，因为逻辑函数可微分并且能求梯度。这是一方面，还有其他，也就是它的输出是浮点值，而不是非0即1。

为什么多层网络有用？

理解了单神经元是如何工作之后，让我们继续探索神经网络是怎么通过多层网络结构学习数据间的复杂关系。理解这一点之前，先来看一个 XNOR函数的例子，回顾一下， XNOR函数的真值表如下：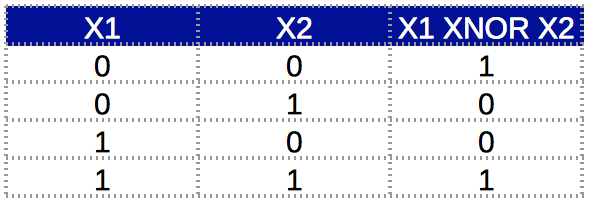
Alt text

表中可以看出，只有当输入相等时输出才等于1，否则，等于0。这种关系不能用单个神经元建模（不相信？不信试试！），因此接下来我们会用多层网络，使用多层网络的核心思想是复杂关系可以被分解为多个简单的函数。
我们来分解下XNOR函数：

注意： ‘+’ 指 OR， ‘.’ 指 AND

现在我们可以使用任何一个简化的例子来实现它。接下来将演示如何使用2个实例去实现XNOR函数。

实例：$X_1 \ XNOR \ X_2 = (A’.B’) + (A.B)$

这里的难点就在于怎么设计一个神经元去模拟实现$A’.B’$，可以用以下方式：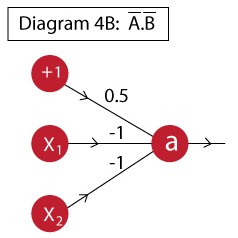
Alt text
该神经元对应的输出是：

它对应的真值表为：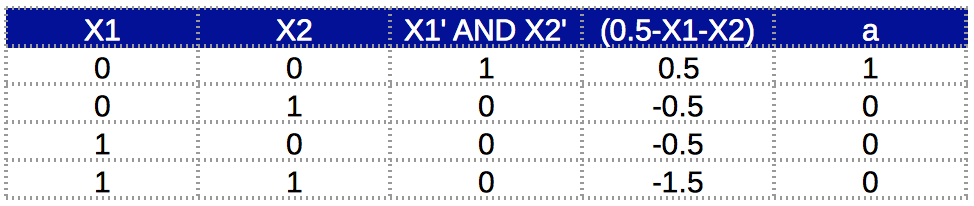
Alt text

现在我们已经对各个分函数进行了建模，接下来我们可以使用多层网络对它们进行组合。首先，看看该神经网络结构的语义图：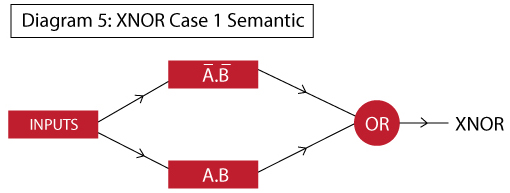
Alt text

可以看出，在第1层中，我们将分别实现$A’.B’$和$A.B$，在第2层，我们将使用它们的输出实现一个OR函数。这样将完成整个神经网络过程，最终的网络将如下所示：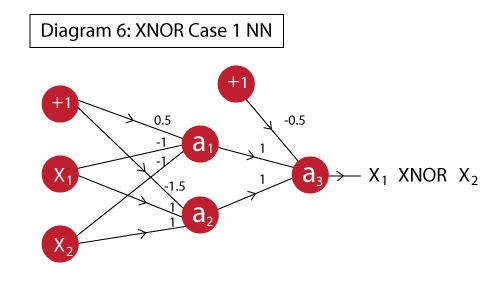
Alt text

如果你仔细观察会发现，上图只不过是我们已经绘制的不同神经元的组合。不同的输出代表不同的单元：

  • $a_1$：实现$A’.B’$
  • $a_2$：实现$A.B$
  • $a_2$：实现$a_1$和$a_2$的OR函数，也就是有效实现$ (A’.B’ + A.B)$

该函数可以使用以下真值表进行验证：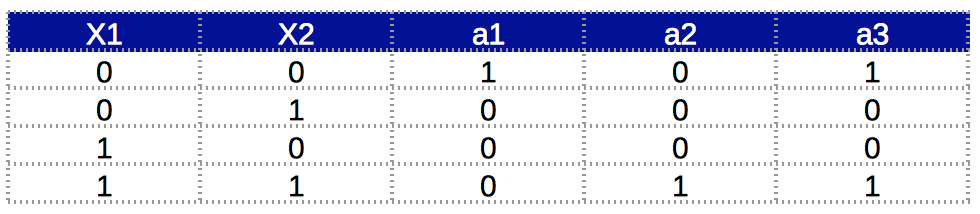
Alt text

通过上述例子应该大概了解了多层神经网络是如何工作的，我们接下来再实现另一情况。

实例：$X_1 \ XNOR \ X_2 = NOT[(A + B) . (A’ + B’)]$

上例中，我们必须单独计算$A’.B’$。如果想直接用基本的AND，OR，NOT函数来实现函数，该怎么办呢？考虑以下语义图：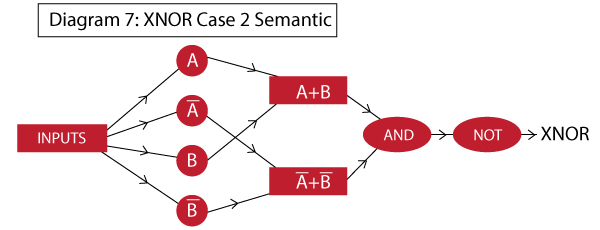
Alt text

这里，可以看到我们不得不使用3个隐藏层。和之前的过程类似，该网络看起来像：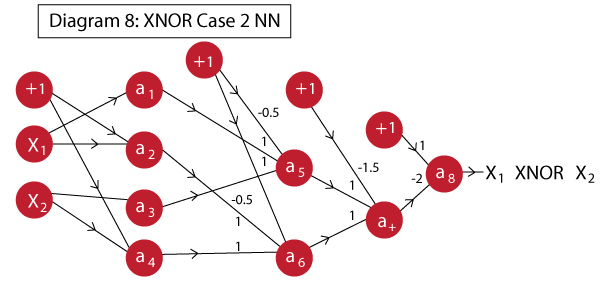
Alt text

这里神经元执行以下操作：

  • $a_1$: 同A一样
  • $a_2$: 代表A’
  • $a_3$: 同B一样
  • $a_4$: 代表A’
  • $a_5$: 实现OR函数，指的是$A + B$
  • $a_6$: 实现OR函数，指的是$A’ + B’$
  • $a_7$: 实现AND函数，指的是$(A + B).(A’ + B’)$
  • $a_8$: 实现NOT函数，指的是$NOT[(A + B).(A’ + B’)]$，就是最终的XNOR函数

注意，通常情况下，神经元会传送到下一个层的除偏置项之外的其他每个神经元。而在此例中，我已经忽略了从第1层到第2层的几个连接，这是因为它们的权重为0，添加它们会使得在视觉上不太好表达。
对应的真值表如下：
Alt text

最后，我们成功实现了XNOR函数，这种方法比情况1更复杂。因此，应该首选情况1的结构。但这里的核心思想是想展示如何将复杂的函数分解成多个网络层次，于是多层网络的优势在此就凸显出来了。

神经网络的一般结构

本节，我们来看一些基本的例子，让我们定义一个神经网络的通用结构。我们还会看到根据给定输入来计算输出的过程，该过程也称为前向传播过程。
通用神经网络可以定义为：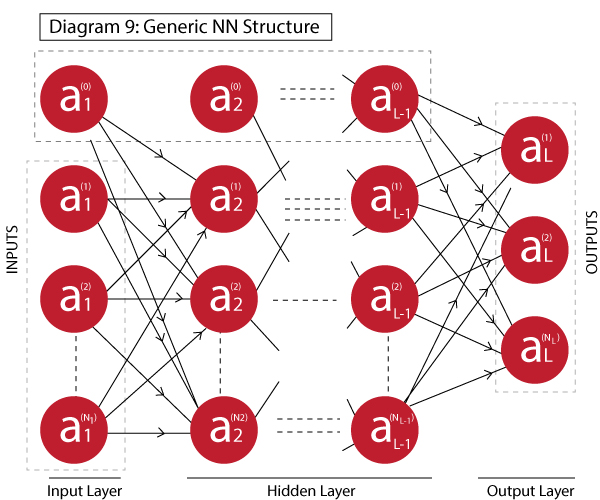
Alt text

它总共有L层，包括1个输入层，1个输出层和L-2个隐藏层。一些术语如下：

  • L：网络的层数
  • $N_i$：第i层网络的节点数量，除了偏置项，其中i=1,2,…,L
  • $a_i^{(j)}$：第i层网络的第j个节点的输出，其中i=1,2,…,L，j=0,1,2,…$N_i$

由于每层网络的输出构成了下一层网络的输入，下面我们利用第i层网络的输出来定义第i+1层网络的输出公式。
第i+1层网络的输入如下：

从第i层网络到第i+1层网络的权重矩阵为：

那么。第i+1层网络的输出可以被计算为：

对于每一层网络使用上述公式，我们就可以得到最终的输出。输出层的节点数量依具体的问题而异，对于回归预测或者二分类问题输出节点可以是1个，对于多分类问题则可以是多个。

上述只是通过一轮迭代得到最终的输出。模型的最终目标则是更新权重，以最大限度地减少损失函数，权重的更新会使用接下来要介绍的反向传播算法。

反向传播（非常重要）

反向传播（BP）算法的工作原理是确定输出端的损失（或误差），然后将其传播回网络，更新权重，以最小化每个神经元产生的误差。接下来不会详细介绍算法，但会试着给一些关于它如何运作的例子。

最小化误差的第一步是计算每个节点关于最终输出的梯度。由于这是一个多层的网络，因此计算梯度没那么直接。

我们来了解下多层网络的梯度，抛开神经网络不讲，先考虑一个非常简单的结构，如下所示：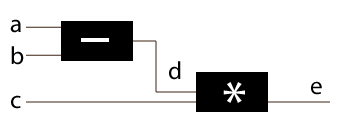
Alt text
该结构有三个输入，满足：

现在，我们要求解a,b,c,d关于输出e的梯度，这很直接就能得到：

然而，为了计算a,b关于e的梯度，我们要用到链式法则：

因此，节点的梯度可以通过该节点输入时的梯度乘以接下来输出时的梯度计算得到，仔细看几遍上述公式，就可以理解。

然而，实际应用中没这么简单。我们再来看看另外一个例子。考虑一个节点被传入给下一层多个节点的情景，而这种情况在神经网络中也是经常存在的。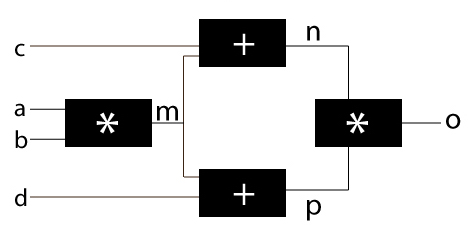
Alt text

这种情况下，除了节点m，其他节点的梯度和上面一样都很容易计算得到，因为m被传输给两个节点了。在此，我将介绍如何计算m的梯度，其余部分自行参照计算。

可以看到，目标梯度是两个不同梯度的总和，我想大家应该看明白了，好好理解一下，接下来继续。先总结下优化一个神经网络的整体过程，每次迭代时需要做的事情如下：

  • 确定一个神经网络结构，包括隐藏层的层数，每一层网络的节点数量，以及激活函数。
  • 随机初始化权重系数。
  • 通过前向传播计算输出。
  • 利用真实标签计算模型的误差。
  • 将误差反向传播到网络，并计算每个节点的误差。
  • 通过更新权重系数以最小化梯度。

至此，我们已经介绍了1-3点，第5点也有所了解。接下来我们来关注4-6点，我们将采用第四小节同样的神经网络结构。

点4-模型的误差

上式中，$y^{(i)}$ 是训练样本的实际输出。

点5-误差反向传播到网络

首先，第L-1层网络的误差可以通过下式计算得到：

其中，i = 0,1,2,…$N_{L-1}$（L-1层网络的节点数量）
小节过半，来看下一些概念：

  • 我们知道一个节点的梯度是它下一层网络所有节点梯度的函数。在此，一个节点产生的误差是基于他下一层网络所有节点误差的权重和，而该节点的输出也组成了下一层网络的输出。由于误差又是通过计算节点的梯度得以优化，因此梯度的影响显而易见。
  • $f’(x)^{(i)}$ 是指变量关于激活函数的导数。注意，x指的是该层所有节点的加权和。
  • 链式规则在这里排上场了，乘上了当前节点的梯度，也就是$f’(x)^{(i)}$与下一层网络节点组合（方程的第一部分）的相乘。

上式需要从第L-1层到第2层连续重复计算，记住，第一层就是训练样本本身。

点6-更新权重系数以最小化梯度

用以下规则更新权重系数：

其中，

  • $l = 1,2,…,(L-1)$，指网络层数的索引（除了最终的输出层）。
  • $i = 0,1,…N_l$，指第l层网络的节点索引。
  • $k = 1,2,…N_{l+1}$，指第l+1层网络的节点索引。
  • $W_{ik}^{(l)}$ 指的是从第l层的第i个节点到第l+1层网络的第k节点的权重。

上式是非常明确的，如有不懂的地方，我建议多看几遍。

结束语

本文的重点是神经网络的基本原理及其工作原理。希望大家现在能理解一个神经网络是如何工作的，从而再也不会把它当作一个黑盒子，一旦你理解了，实际上也很容易，期待着与您进一步交流！

参考文献：https://www.analyticsvidhya.com/blog/2016/03/introduction-deep-learning-fundamentals-neural-networks/

-------------本文结束感谢您的阅读-------------
友情提示: 转载请保留原文链接及作者。

感谢支持、勇于创作