动态定价-解读Airbnb使用的模型

随着饭点儿业务流量不断的提升，预购产品在未来可期范围必将深入行业，技术的支撑应该提前做出响应，在此和大家一起探讨一下基于动态定价思路的折扣推荐方案。

• 饭点儿-最新业务发展基本情况

• 饭点儿-预购产品示意图

什么是动态定价？

动态定价(Dynamic pricing)是指企业根据市场需求和自身供应能力，以不同的价格将同一产品适时地销售给不同的消费者或不同的细分市场，以实现收益最大化的策略。

• 基于时机定价策略：
  关键在于把握顾客不同时间对价格承受的心理差异。
  高峰负荷定价（peak-load pricing）：供不应求，供应缺乏弹性，应合理提价
  清理定价（clearance pricing）：需求状况不确定、容易贬值，须降低价格，及时清理多余库存。
• 基于市场细分与限量配给策略：
  根据不同的产品配置、渠道、客户类型和时间等，进行区别定价，如：航空公司。
• 基于动态推销策略:
  利用互联网赋予的强大优势，根据供应和库存水平的变化，迅速、频繁地实施价格调整，为顾客提供不同的产品、各种促销优惠、多种交货方式以及差异化的产品定价。例如，在亚马逊购书，书店会根据消费记录，给与个性化的购书建议。
• 基于三种动态定价的综合运用
  在实际运用过程中，可酌情考虑单独实施某一策略，或进行策略组合。顾客价格承受心理差异性越强，市场需求的不确定因素越多，这些策略的价值及其作用也就越大。

好文解读-Customized Regression Model for Airbnb Dynamic Pricing

文章来源：Peng Ye, Julian Qian, Jieying Chen, Chen-hung Wu, Yitong Zhou, Spencer De Mars, Frank Yang, and Li Zhang. 2018. Customized Regression Model for Airbnb Dynamic Pricing. In KDD ’18: The 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, August 19–23, 2018, London, United Kingdom. ACM, New York, NY, USA, 9 pages. https://doi.org/10.1145/3219819.3219830
Airbnb是一个用于共享住宿的在线平台，在这里寻求住宿的客人和有空余房间共享的主人可以完成在线匹配。

本文详细介绍了Airbnb用于向房主提供建议价格的方法（房主最终仍然控制着Airbnb平台的定价）。提出的模型已在Airbnb部署生产超过1年。模型的第一次迭代的推出为预订价值带来了显著收益。

本文提出的方法

在理想情况下，为了使得利润最大化，我们一般会估计一个需求函数F(P), 即在给定价格P的情况下估计房间的需求量，之后选择P的值，使P×F(P)的值最大。但针对Airbnb需求函数不仅仅和价格有关，应该是F(P, t, id)，其中t是时间，id代表独立的房间。时间上因素上，需求受季节性和特殊事件的影响，以及预定早晚的影响。另外，Airbnb上房子各有不同，房子评分、浏览量等一些因素也导致需求函数的变化。而且，由于Airbnb并不是直接控制房间价格的，而是只能给出“建议价格”，所以想要直接拿不同的定价策略做实验来观察市场反应也是不容易的。

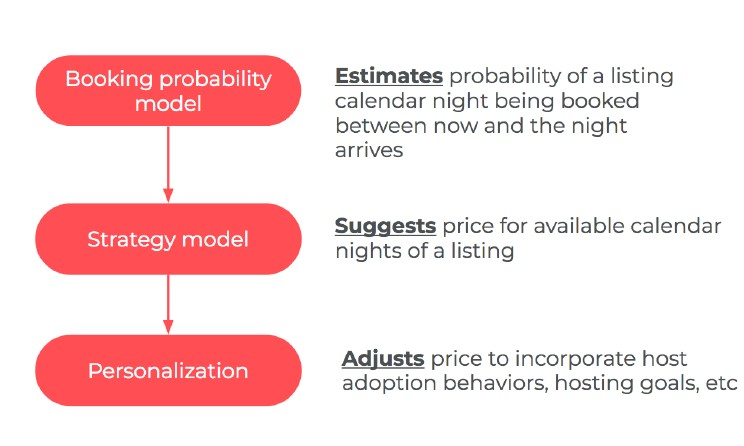
Airbnb最终确定的定价系统有三个组成部分：

• 首先构建一个基于Gradient Boosting Machine (GBM)的预定概率模型，用于预测某一晚某房间被预定的概率。
• 然后这些预测结果会被作为特征输入到定价策略模型，对空闲日期提出建议价格。
• 最终策略模型会加入其他个性化逻辑，以符合房东的目标、结合特殊事件等等。
  

预定概率模型

想知道某间房会有多大概率被预定，这里是用的是Gradient Boosting Machines(GBM)模型，是一个二分类的问题。除了对全局样本通过GBM训练建模以外，也给每个市场训练单独的模型，训练数据的抽样率根据市场密度而变化，这些模型考虑了三种不同类型的特征：

• 房屋属性特征：每晚的房价，房间类型，人数，卧室/浴室数量，设施，位置，评论，历史入住率，是否启用即时预订等
• 时间特征：季节因素、可入住时长、预定早晚等。
• 供给特征：周围房屋情况、浏览量、搜索率等。

通过在一定范围内的不同价格点对预订概率模型进行评分，可以获得估计的需求曲线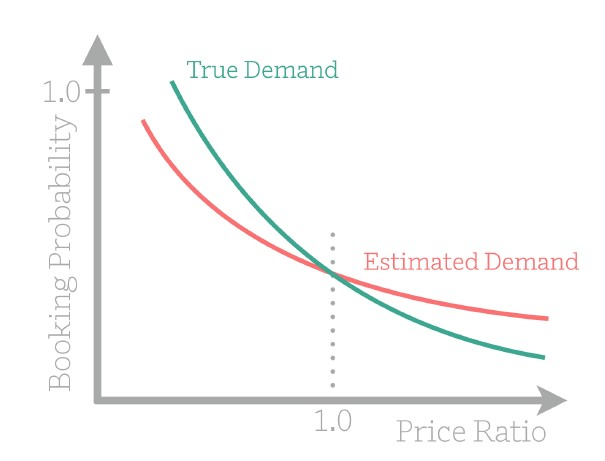

但是，由于上述的特征影响因素太多，想得到精确的需求曲线进行价格设置是非常困难的。主要的影响分三类：

• 数据稀疏性：大部分房屋都不怎么会经常调整价格，而且变化基本都在一个小范围，因此难以获得比较偏的观察样本。
• 样本唯一性：由于房屋的独特性，难以通过学习提高模型泛化性。
• 特征共线性：不可避免，很多特征都和价格有关，比如搜索率、浏览量、预定占比等等

尝试了直接应用利润最大化策略，但是A/B测试结果显示这些方法在实际中通常会失败。所以，我们决定找其他的替代方法。替代法使用预定概率模型的输出结果作为定价策略模型的输入因素之一。

定价策略模型

首先让我们思考：在缺少最优价的基础上，训练定价策略模型时，应该用什么评估尺度呢？假设P为实际房间一晚的价格，Psug为建议价格，最优价格为P0（如果存在），我们认为以下情况Psug是不好的：

• 当房间被预定了且Psug < P
• 当房间没有被预定且Psug >= P

还有两种情况不能确定建议是好是坏：

• 当房间被预定了且Psug >= P
• 当房间没有被预定且Psug < P

Item	Booking	Non-Booking
Psug >= P	a	b
Psug < P	c	d

定义以下几种度量：

• Price Decrease Recall (PDR)：所有没有被预定的样本中，建议价格低于实际价格的比例 $$PDR = \frac{d}{b + d}$$
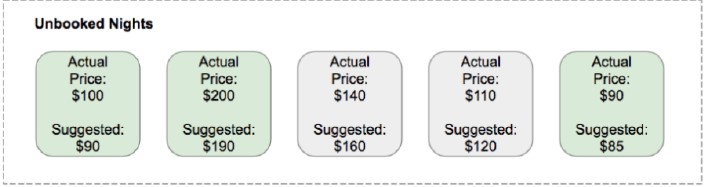
  如上图例子，PDR = 0.6
• Price Decrease Precision (PDP)：所有Psug < P的样本中，没有被预定的房间比例 $$PDP = \frac{d}{c + d}$$
• Price Increase Recall (PIR)：所有被预定的样本中，建议价格高于或等于实际价格的比例 $$PIR = \frac{a}{a + c}$$
• Price Increase Precision (PIP)：所有Psug >= P的样本中，被预定的房间比例 $$PIP = \frac{a}{a + b}$$
• Booking Regret (BR)：预定反悔率，所有被预定的样本中，取零和预定价格与建议价格之间差的百分比之中的最大值，然后从这些值中取中位数 $$BR = median_{bookings}(max(0, \frac{P - Psug}{P}))$$
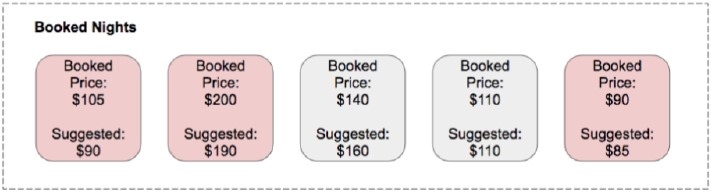
  如上例子，BR = Median(14%,5%, 6%, 0, 0) = 5%。本文采用PDR和BR两个度量作为评价指标。

目标函数

给定N个训练样本${xi, yi}_{i=1}^N$，其中，$xi$代表关于房间特征的输入，$yi$代表预定状态，1为预定，0为未预定。特征$xi$包含以下内容：

• 房主设定的价格$P_i$。
• 上面预定概率模型得出的房间被预定的概率$q_i$
• 市场需求信号：这有利于模型对市场动向做出及时反应。

对于$xi$来说，建议价格定义为$f_\theta(xi)$，$\theta$为需要学习的参数集合，自定义的损失函数受启发于SVR中$\epsilon$-不敏感损失函数，虽然我们不知道真实的最优价格，但是可以根据实际情况定义一个合理价格的区间，认为最优价格应该落在其中。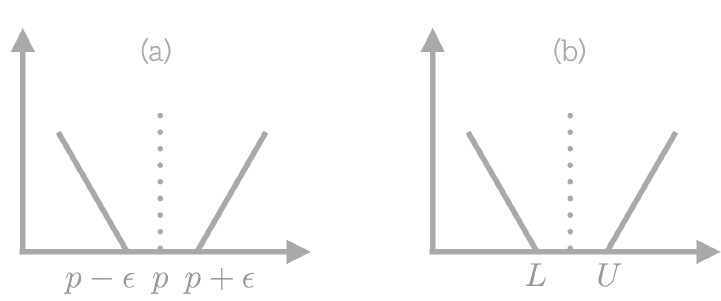

损失函数如下：

$$L = arg min_\theta \sum_{i=1}^N (L(P_i,y_i) - f_\theta(x_i))^+ + (f_\theta(x_i) - U(P_i,y_i))^+$$

其中，“+” 表示 $max(0, \cdot)$，$L(P_i,y_i)$ 、$U(P_i,y_i)$分别表示最优价格区间的上界和下界，如果建议价格落在上界和下界之间，那么损失=0，否则，损失等于建议价格与界限的距离，上界和下界分别定义为：

$$L(P_i,y_i) = y_i \cdot P_i + (1 - y_i) \cdot c_1P_i$$ $$U(P_i,y_i) = (1 - y_i) \cdot P_i + y_i \cdot c_2P_i$$

其中，$c_1 \in(0,1)$，$c_2 > 1$，下图分别说明了损失函数在正负样本情况下的变化方向。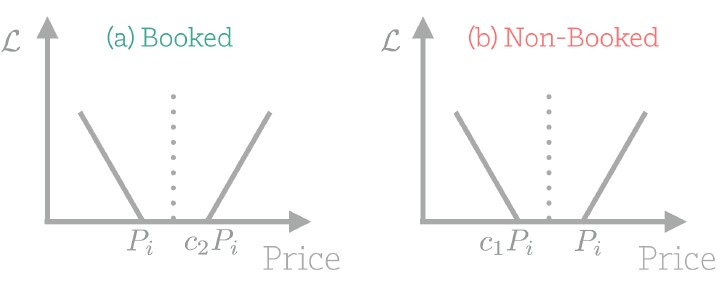

对于正样本来说，当建议价格落在区间$(P_i, c_2P_i)$时，损失函数会降为0，与此同时预定反悔率BR也达到最小0。同样，对于负样本来说，当建议价格落在区间$(c_1P_i, P_i)$时，损失函数会降为0，与此同时PDR会很大因为建议价格比实际价格要低，这也正是模型想发展的方向。

需求增强定价法

本节着重给出建议价格的具体形式，模型的背后需要满足几个前提条件的：

• 对于同一个房间，建议价格和被预定概率是正相关的，这样建议价格才能对概率的变化做出调整。
• 建议价格往往是集中在房主喜欢设定的最有代表性的价格之间左右徘徊，通过学习增加/降低的力度去控制。
• 预定概率模型捕捉不到的额外需求信号，应该加以关注。

基于上述假设，引入一个非对称指数模型，通过样本数据学习对实际价格的增加/减少度，建议价格Psug表示如下：

$$Psug = P \cdot V$$

其中，增加/减少度V定义如下：

$$V = \begin{cases} 1 + \theta_1(q^{\varphi_H^{-qD}} - \theta_2) & \text{if $D$ > 0} \\ 1 + \theta_1(q^{\varphi_L^{-(1-q)D}} - \theta_2) & \text{if $D$ <= 0} \end{cases}$$

• P为房主设置的代表性价格（比如：历史被预定价格的中位数）。
• q为当价格为P时的预定概率模型得出的概率。
• D是根据簇集合的附加需求信号计算的需求分数（簇是一组类似的房间样本）。
• $\theta_1$控制价格增长/缩减的速度。
• $\theta_2$控制何时建议原始的价格
• $1 < \varphi_L < \varphi_H < 2$ 是两个不同的常数，用于分别控制价格涨跌时需求曲线的弯曲程度，不同的常数希望模型训练能够非对称地去学习参数。

另外，需求得分D是被归一化的，D值越高，相应簇集合的需求就越高，给定$\theta_1$和$\theta_2$，Psug随着预订概率q单调递增，这保证了我们建议对于预订量较高的夜晚提供更高的价格。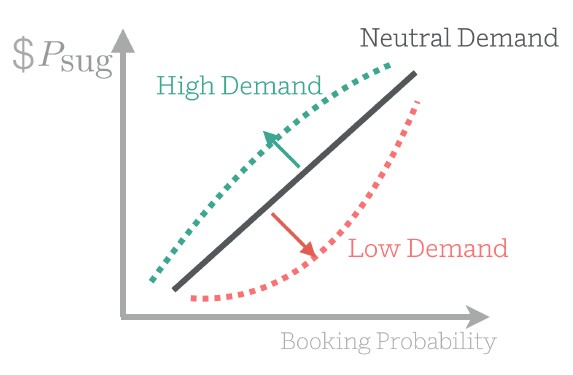

通过对上式求导可知：

$$\frac{\partial V}{\partial \theta_1} = q^{\varphi_H^{-qD}} - \theta_2$$ $$\frac{\partial V}{\partial \theta_2} = -\theta_1$$

该公式为参数学习提供了良好的型式，进而最终可以求出Psug。

模型训练

• 样本层级的训练：Airbnb上的房间价格可能彼此不同，即使是属于同一类型和市场的房间。并且每个房间的最优策略也很大程度上受其自身属性和房主偏好的影响。所以，不像预定概率模型可以分区域训练，定价决策模型需要对每个房间样本单独进行训练，参数$\theta_1$和$\theta_2$是在Airbnb上400多万个有效房源中训练出的，训练更关注最近的预定行为，从而更好地反映季节信号。但同样会基于市场和全局去做训练，特别是当单个房间样本信息不足的时候，比如从来没有被预定过的房间。
• 参数约束：引入参数约束来保证定价结果在合理的范围内 $$l_1 <= \theta_1 <= \mu_1$$ $$l_2 <= \theta_2 <= \mu_2$$ 其中，$(l_1,l_2,\mu_1,\mu_2)$ 被作为一个箱子约束去控制参数的范围。比如，在真实实验中，会发现当$\theta_1$特别大时建议价格不稳定，$\theta_2$特别大时价格增长很小，这些情况都不是房主想看到的。
  特别地，对于一些小需求的样本，可以有如下约束： $$a\theta_1 + b <= \theta_2 (a > 0)$$ 意思是，当$\theta_1$特别大的时候，$\theta_2$也应该同比例放大，以限制高建议价格的产生频次。这些约束通常被视为故障保险和特殊情况处理机制，以避免出现提出不切实际的建议价格。
• 算法+计算：Stochastic Gradient Descent（SGD），Spark
• 训练样本

实验结果

• 数据集采样：
  ds：代表使用模型预测的日期（当前日期）
  ds_eval：代表收集到预定标签状态的日期（未来日期）
  ds_night：代表售卖日期
  在ds与ds_eval期间，至少被预定了一次以及可待预定的房间视为正样本；一次都没有被预定且 ds_night <= ds_eval的情况视为负样本。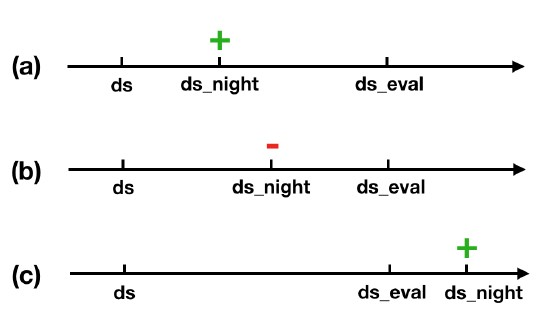
  

离线和在线评估结果表明，所提出的策略模型的性能明显优于直接最大回报定价策略，定价策略模型显著改善了PDR和BR。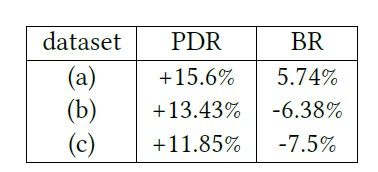

除了定量评估，论文作者还检查了2018年2月8日生成的未来120晚的价格，下图分别是针对日本东京和美国加州太浩湖的房源价格走势：
Tokyo：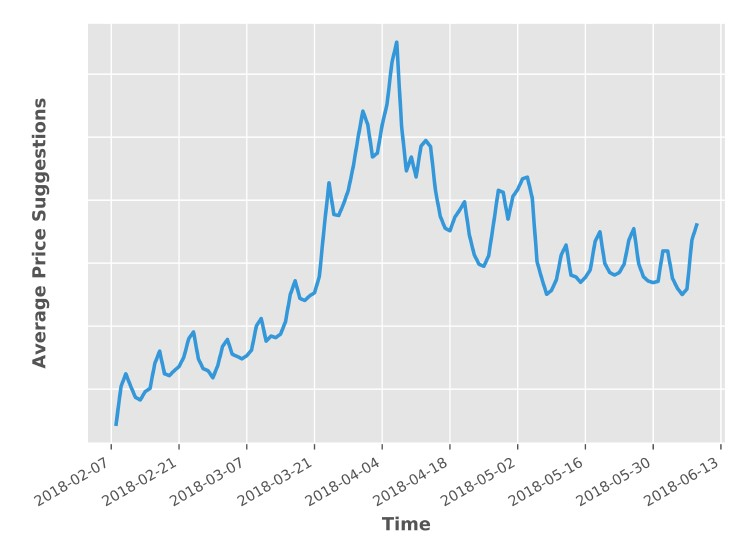

Tahoe, CA：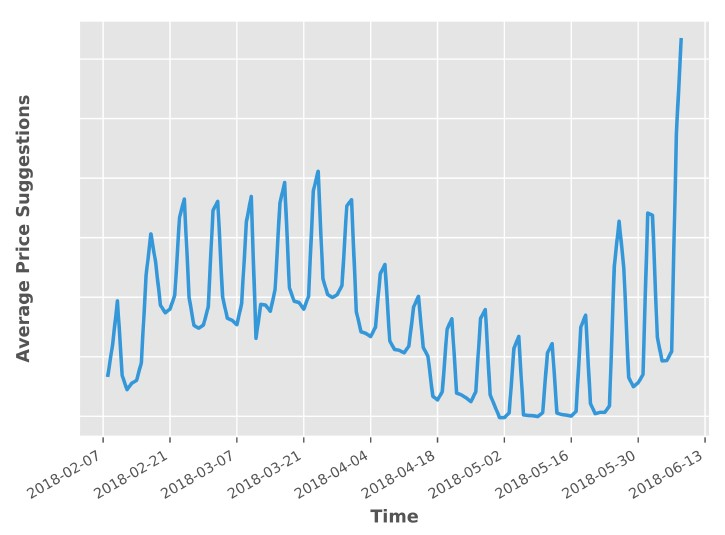

可以看到，两地房间的价格都在周末有所上升，并且东京在三月末到四月初的房价也相对较高，因为那正是赏樱的好时节。“从这两个案例中，我们看到模型的确能捕捉到时间带来的房价波动”