模型偏差(Bias)和方差(Variance)的权衡对模型的整体性能至关重要。
模型目标函数包含下面两项:

Bias(偏差)
描述的是预测值的期望与真实值之间的差距,针对的是单个模型,偏差越大,越偏离真实数据,刻画得是模型的拟合能力。
Variance(方差)
描述的是预测值的变化范围,离散程度,也就是离其期望值的距离。方差越大,数据的分布越分散。度量了训练集的变动所导致的学习性能的变化,即数据扰动造成的影响,方差可以理解为多个模型之间的差异,刻画的是模型的复杂度。
感性理解
目标函数的设计来自于统计学习里面的一个重要概念叫做Bias-variance tradeoff。Bias可以理解为假设我们有无限多数据的时候,可以训练出最好的模型所拿到的误差。而Variance是因为我们只有有限数据,其中随机性带来的误差。目标中误差函数鼓励我们的模型尽量去拟合训练数据,这样相对来说最后的模型会有比较少的bias。而正则化项则鼓励更加简单的模型。因为当模型简单之后,有限数据拟合出来结果的随机性比较小,不容易过拟合,使得最后模型的预测更加稳定。
Bias-variance tradeoff
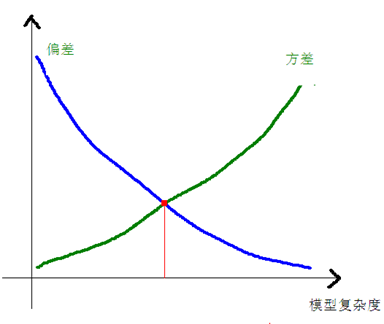
我们为什么要在目标函数中加入偏差和方差?
- 优化损失鼓励预测模型
- 拟合训练数据至少让你靠近的训练数据,希望接近底层分布。
- 优化正规化鼓励简单模型
- 简单的模型在预测未来上往往有较小的方差,预测稳定。
如何处理高Bias高Variance
(1)增加训练样本可以减小方差,随着样本量的增加,泛化性能会好一些,验证损失会逐渐减小,所以会减小方差。
(2)取少量的特征,可以有效的防止过拟合,提高泛化性能,会减小方差。
(3)取更多的特征,能从更多的角度学习数据的分布,减小训练损失,会减小偏差。
(4)增加多项式特征,增加了模型的复杂度,可以减小偏差。
(5)减小正则化参数:就是削弱正则的作用,增加模型复杂度,减小偏差
(6) 增大正则化参数:增强正则的作用,对参数进行有效控制,防止过拟合,减小方差。
参考:
http://www.52cs.org/?p=429
https://www.jianshu.com/p/9d5c5376cacb

